Vocabulaire Statistique
Metrics & Decisions

Dans ce 5è numéro de K-Insights, vous découvrirez le vocabulaire statistique* usuel.
* Sans aucune prétention de l’exhaustivité : Ce que nous présentons ici sont des concepts de base.
1. Population statistique

C’est un ensemble fini d'objets (individus ou unités statistiques) sur lesquels porte une étude et dont les éléments répondent à une ou plusieurs caractéristiques communes.
Cet ensemble est défini avec précision et sans ambiguïté. En effet, une population statistique est déterminée à partir de quatre facteurs :
- Sa nature (Humains, Parcelles, Animaux, Entreprises, etc.)
- Ses caractéristique (Sexe, Age, Superficie, Chiffre d’affaires, etc.)
- Sa localisation (Ville, Commune, Forêt, ZOO, etc.)
- La date d'observation
 Ex : Les étudiants orientés en faculté d’économie à l’université d’Abidjan en 2021
Ex : Les étudiants orientés en faculté d’économie à l’université d’Abidjan en 2021
2. Individu ou unité statistique
Il s’agit simplement de chaque élément de la population statistique.

Ex : Un étudiant de la faculté d’économie de l’université d’Abidjan en 2021
3. Echantillon
C’est un sous-ensemble d’unités statistiques censé être représentatif d'une population statistique. L'objectif est d'obtenir une meilleure connaissance de la population par l'étude du seul échantillon.

Le recours à un échantillon répond en général à une contrainte pratique (manque de temps, coût financier, ...) ne permettant pas l'étude exhaustive de la population.
4. Echantillon représentatif
Un échantillon est dit représentatif lorsqu’il possède les mêmes caractéristiques que la population statistique que l’on souhaite étudier.
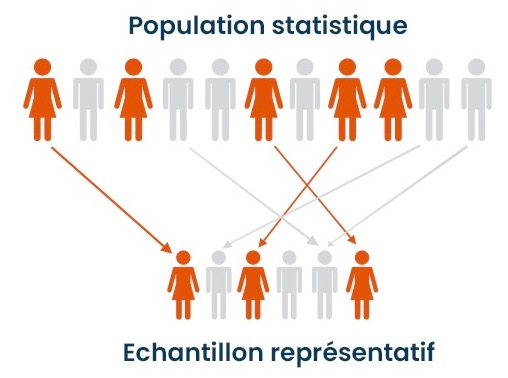
L'acte de sélection de cet échantillon s'appelle l'échantillonnage.
5. Observation
C'est l'expérience de sélection ou de recueil d'information sur un phénomène ou une unité statistique.

La donnée n'est rien d'autre que le résultat de l'observation.
6. Variable statistique
Sur une population statistique, on étudie un caractère, c’est-à-dire que, pour chaque unité statistique, on observe la présence d’un caractère appelé variable statistique.

Cela consiste à identifier et à classer les individus en sous-ensembles.
Une variable statistique peut présenter une ou plusieurs situations différentes ( modalités) qui doivent remplir trois critères :
- Exhaustivité : Toutes les situations possibles sont identifiées
- Incompatibilité : Un individu ne peut présenter plus d’une modalité.
- Sans ambiguïté : Les modalités doivent sont définies sans ambiguïté.
Ex : La variable Sexe dont les modalités connues sont Masculin et Féminin
Il existe deux types de variables statistiques.
6.1 Variable quantitative ou numérique
Elles s’expriment par des nombres (longueur, durée, coût, etc.).
On distingue les variables quantitatives discrètes et les variables quantitatives continues :
- Une variable quantitative est discrète si elle ne prend qu’un nombre fini de valeurs isolées (Ex : le nombre d’enfants par femme).
- Une variable quantitative est continue si elle prend toutes les valeurs possibles à l’intérieur d’un intervalle (Ex : la taille).
6.2 Variable qualitative ou catégorielle
Elles s’expriment par l’appartenance à une catégorie (couleur, sexe, catégorie socio-professionnelle, etc.).

On distingue les variables qualitatives ordinales et les variables qualitatives nominales :
- Une variable qualitative est ordinale s’il est possible d’établir une relation d’ordre entre ses modalités (Exemple : La mention au BAC, le niveau de satisfaction).
- Une variable qualitative est nominale lorsqu’il n’est pas possible d’établir un ordre entre ses modalités (Exemple : le sexe, la nationalité).
7. Distribution statistique
C’est la donnée des couples (modalité, fréquence) de cette variable. Autrement dit, pour chaque valeur possible de la variable, on associe sa fréquence d’apparition dans la population.
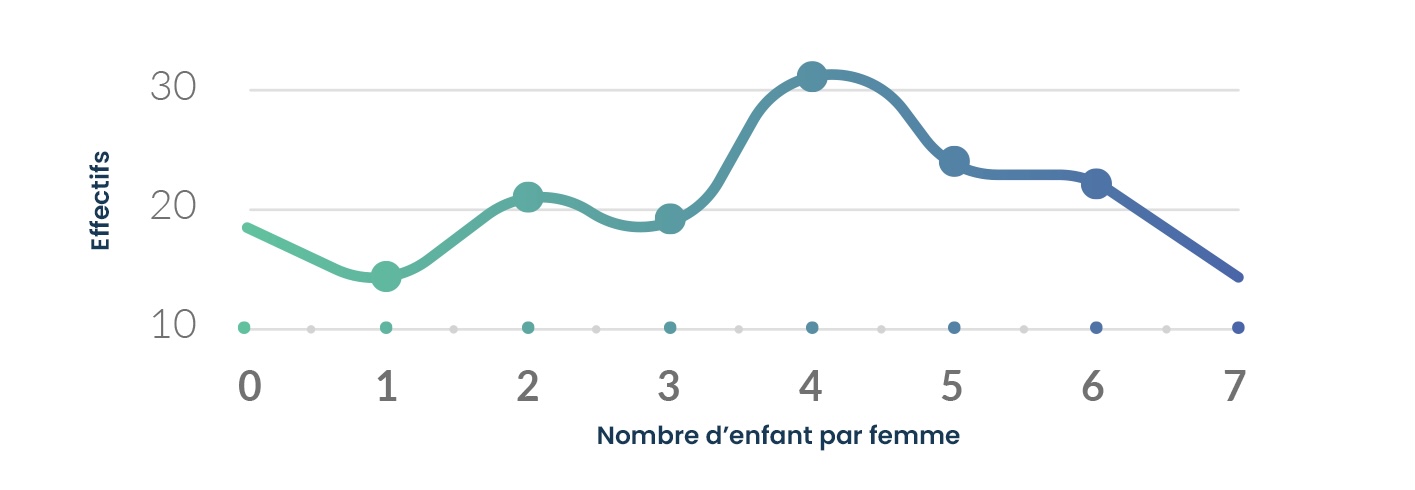
8. Indicateur de tendance centrale ou de position
Le but est de donner un ordre de grandeur général des observations i.e une valeur unique qui résume au mieux les données.
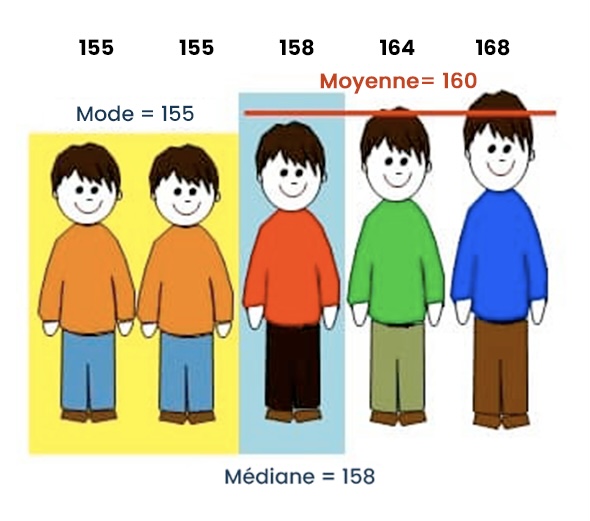
- Le mode : C’est la valeur de la variable pour laquelle la fréquence absolue (effectif) ou fréquence relative (pourcentage) est la plus élevée.
- La médiane* : C’est la valeur de la variable qui partage la série des individus en deux ensembles d‘effectifs égaux.
- La moyenne* : C’est la valeur qu’aurait chaque individu si le partage était équitable.
* Uniquement pour les variables quantitatives
9. Indicateur de dispersion*
Il est nécessaire de compléter les indicateurs de tendance centrale par des indicateurs de dispersion, qui donnent une idée sur la variabilité des données.
* Uniquement pour les variables quantitatives
- L’étendu : C’est la différence entre la plus grande et la plus petite des données de la série statistique. Elle indique le domaine de variation de la variable statistique.
- La variance : Elle permet de tenir compte de la dispersion de toutes les valeurs d'un ensemble de données. De cette valeur est déduite l’écart type qui est la racine carrée de la variance. L’écart type exprimé la distance moyenne des observations à leur moyenne.
- Le coefficient de variation : C’est le rapport de l’écart type par la moyenne arithmétique. Il permet de comparer plus aisément la dispersion de deux ou plusieurs séries d'observation. La série la plus dispersée est celle qui a le coefficient le plus élevé.
